Suma angulos exteriores de un poligono

Suma de los ángulos exteriores de un pentágono

Para ayudarte a ver cuál es la suma de todos los ángulos exteriores de un polígono, utilizaremos un cuadrado y después un pentágono regular. Como es muy fácil ver cuál es la suma de un cuadrado, empezaremos por el cuadrado.

Observa que un ángulo exterior está formado por un lado del cuadrado y una prolongación de un lado adyacente.  Por ejemplo, en la figura siguiente, el ángulo x, el ángulo y, el ángulo z y el ángulo w son ángulos exteriores.

Cada ángulo interior de un cuadrado es igual a 90 grados. Observa que un ángulo interior más el ángulo exterior adyacente es igual a 180 grados.Ángulo interior + ángulo exterior adyacente = 180 grados.

De hecho, la suma de ( el ángulo interior más el ángulo exterior ) de cualquier polígono siempre suman 180 grados. Esto es así porque cuando extiendes cualquier lado de un polígono, lo que realmente estás haciendo es extender una línea recta y una línea recta siempre es igual a 180 grados.

En la figura o pentágono anterior, usamos a para representar el ángulo interior del pentágono y usamos x,y,z,v, y w para representar los 5 ángulos exteriores.Para hallar la medida del ángulo interior de un pentágono, sólo tenemos que usar esta fórmula.[(n - 2 ) 180] / n Como n es igual a 5, [(n - 2 ) 180] / n = [(5 - 2) 180] / 5 = [3 x 180] / 5 = 540 / 5 = 108

Ángulo exterior de un polígono

de los ángulos exteriores de un polígono que tiene n lados. Sabemos que, ángulo exterior + ángulo interior adyacente = 180°Entonces, si el polígono tiene n lados, entoncesSuma de todos los ángulos exteriores + Suma de todos los ángulos interiores = n × 180°Entonces, suma de todos los ángulos exteriores = n × 180° - suma de todos los ángulos interioresSuma de todos los ángulos exteriores = n × 180° - (n -2) × 180° = n × 180° - n × 180° + 2 × 180° = 180°n - 180°n + 360° = 360°Por tanto, concluimos que la suma de todos los ángulos exteriores del polígono que tiene n lados = 360°.

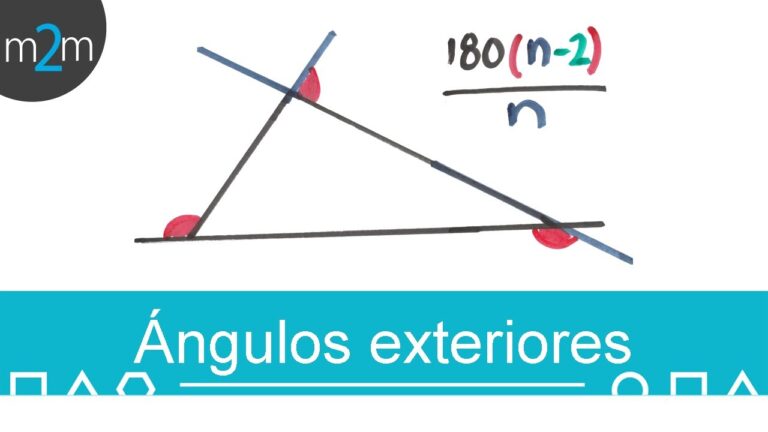
Fórmula del ángulo exterior de un triángulo

Antes de pasar a conocer la fórmula de la suma de ángulos exteriores, recordemos primero qué es un ángulo exterior. Un ángulo exterior de un polígono es el ángulo entre un lado y su lado adyacente prolongado. Esto se puede entender claramente observando los ángulos exteriores en el triángulo de abajo. La fórmula de la suma de ángulos exteriores dice que la suma de todos los ángulos exteriores de cualquier polígono es 360°.

Así, la suma de todos los ángulos exteriores de un triángulo es 360°. Del mismo modo, podemos demostrar que la suma de todos los ángulos exteriores de cualquier polígono es 360°. Así, la suma de los ángulos exteriores se puede obtener a partir de la siguiente fórmula:

Fórmula de la suma de los ángulos exteriores de un polígono

Preguntas y Respuestas¿Cuál es la suma de los ángulos exteriores de un polígono?Last updated date: 02nd Feb 2023-Total views: 263.7kVistas hoy: 4.56kRespuestaVerificada263.7k+ visitasPista: En este problema necesitamos saber que la suma de todos los ángulos interiores en cualquiera de los polígonos es 180(n-2) donde n es el número de lados presentes en el polígono. Consideraremos aquí un polígono cualquiera y lo resolveremos para obtener la suma de los ángulos exteriores del polígono. La respuesta completa paso a paso es: Polígono: Una forma plana (bidimensional) con lados rectos. Ejemplos: triángulos, rectángulos y pentágonos. Un círculo no es un polígono porque es curvo y no tiene lados.Aquí necesitamos encontrar la suma de ángulos exteriores del polígono y en cualquiera de los polígonos la suma de ángulos exteriores es la misma y el procedimiento para encontrarla también es el mismo. Consideraremos aquí el pentágono para hallar la suma de sus ángulos exteriores. El pentágono se puede dibujar como,